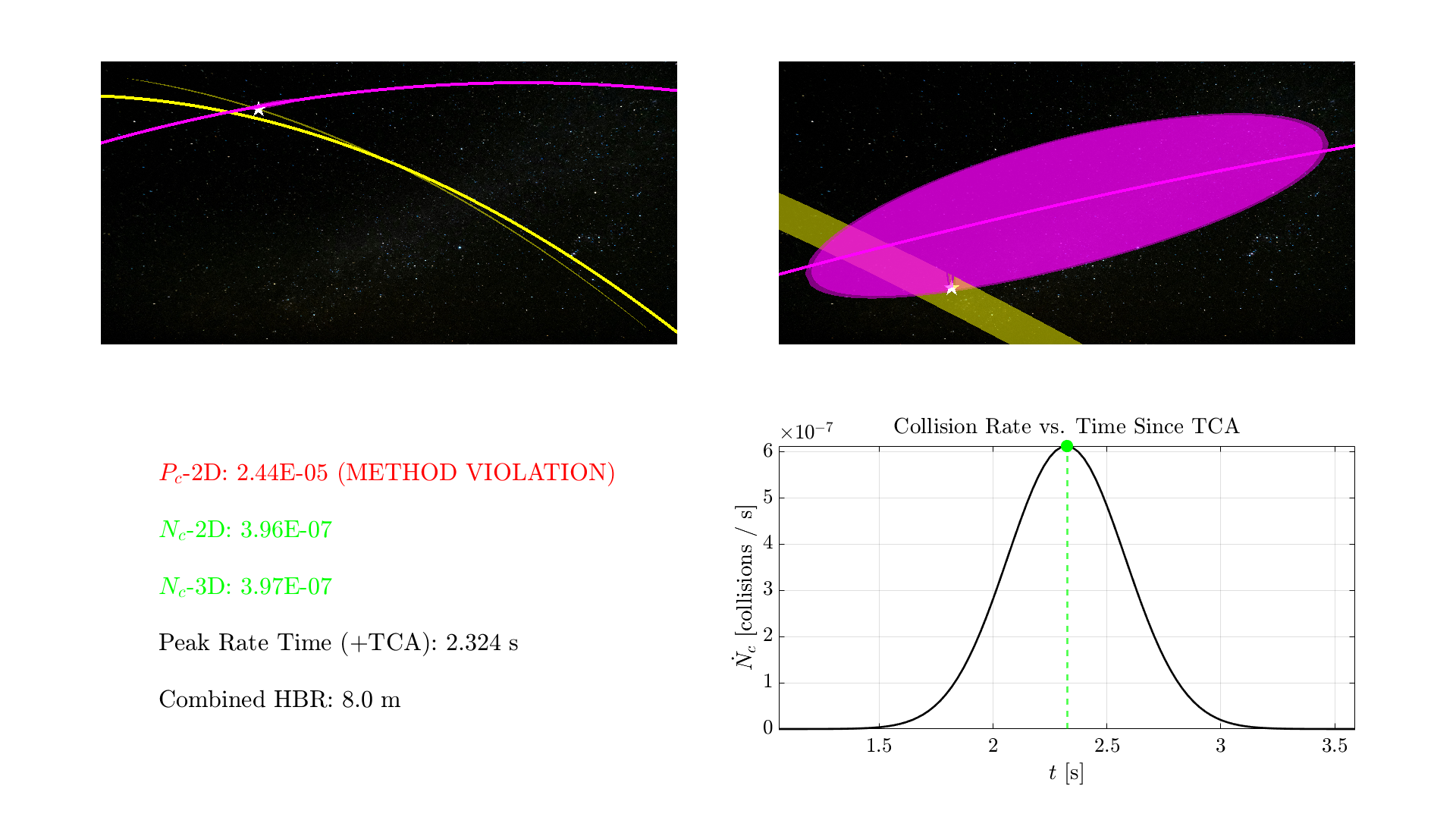
Showcase and Comparison of Three Methods for Visualizing Near-Earth Satellite Conjunction
Events
During my second internship with CARA, I focused heavily on
research, and specifically on developing methods for visualizing satellite conjunctions.
A conjunction is a close approach event between two satellites; these are of interest because an
orbital collision could be devastating to the Low-Earth Orbit environment, so knowing where
satellites are and how they are moving is crucial to keeping space safe and usable.
I built on and developed three methods for showcasing these events, each of which is suited to
different conjunction geometries; I analyzed these cases and paralleled the usage of these
visualization algorithms with the algorithms employed by CARA in predicted a probability of
collision.
From this research, I both programmed the visualizations themselves and wrote a paper (on which I
was first author); the paper was accepted to the 2025
AAS/AIAA Astrodynamics Specialist Conference, which I was unfortunately unable to attend
in-person.
Download my paper here, and download my poster here!
Applications of Computer Vision to Space and Plasma Physics
As part of the Discovery Learning Apprenticeship
program, I was chosen to present my research at an end-of-year symposium in which a panel of
graduate mentors selected top projects from that year's participants.
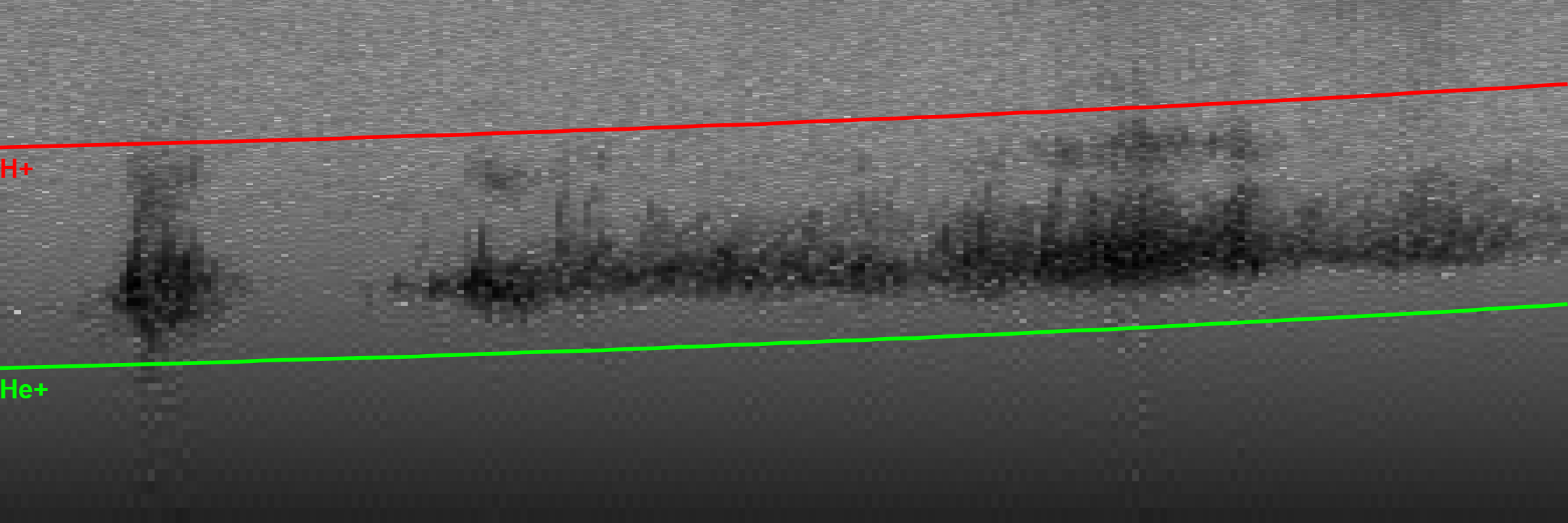
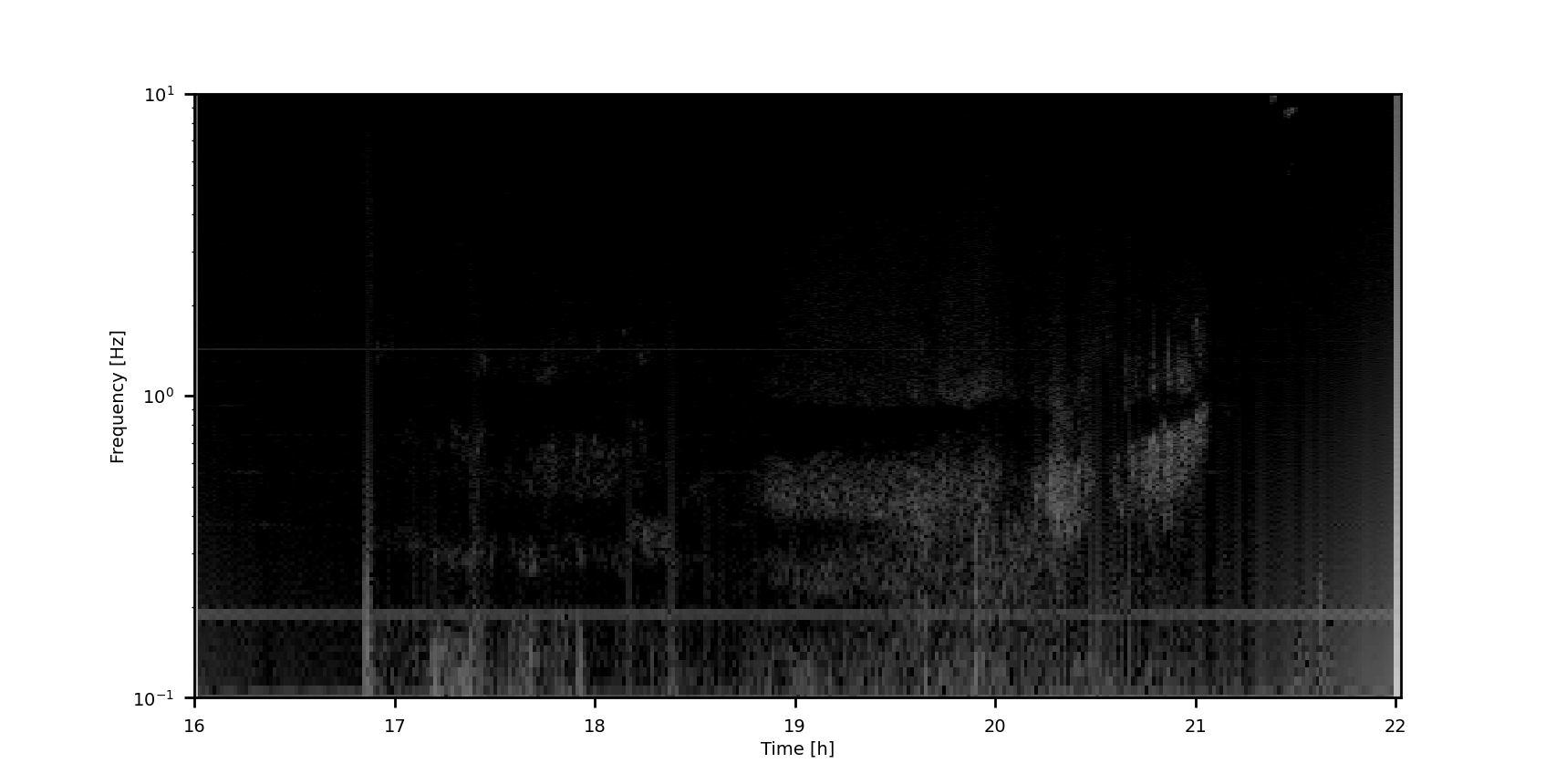
My research focused on the detection of plasma waves in Van Allen Probe data; I had to first devise
a consistent way of visualizing these waves (a challenge due to their low frequencies, as I was
working with electromagnetic ion cyclotron waves), then annotate the spectrograms I created and
develop a computer vision model to reliably detect these waves autonomously.
I achieved an mAP50 of 0.738 with the latest version of the model and began researching the
distribution of these waves in the Earth's magnetosphere; the goal of this was to better understand
their occurrence locations and frequencies and compare those to theoretical models.
Download my poster here!
Analyzing and Solving the N-Body Problem
Following my numerical analysis class, I decided to also take numerical differential equations -
and, similar to numerical analysis, it, too, had a final project that involved building on a topic
we covered in class.
I teamed up with Edward Wawrzynek again, as well as
Bryce Pfuetze, and we decided to tackle the N-body
problem, a common problem across engineering and physics fields.
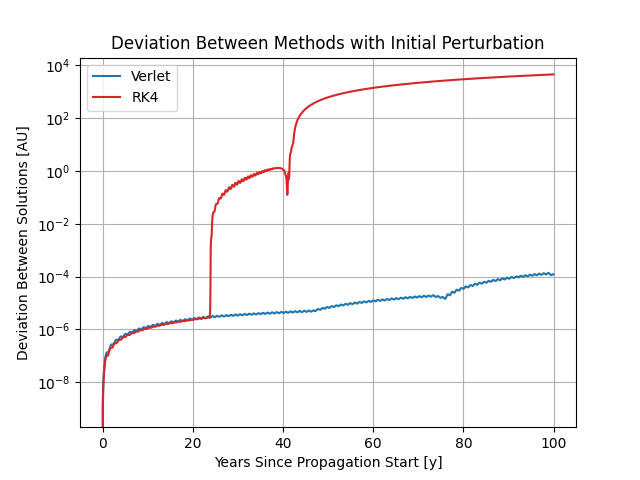
Specifically, since this problem has no analytical solution, we decided to focus on understanding
and tackling the inherent stiffness in the problem; we also studied symplectic integrators and their
useful energy-conservation properties.
We compared our own implementations of the Euler, RK2, RK4, and Stormer-Verlet methods and studied
energy error over time; we also compared integrated ephemerides to those given by the JPL Horizons
database.
This work led directly into my work at the Celestial
and Spaceflight Mechanics Laboratory.
Download our paper here, or check out our code
repository
here!
COMAP MCM 2025
Once again, Elizabeth Cutting,
Madison Jones, and I decided to compete in a mathematical modeling
competition - this time, in the
Mathematical Contest in Modeling, a more math-heavy
variant of the
Interdisciplinary
Contest in Modeling we partook in in 2023.
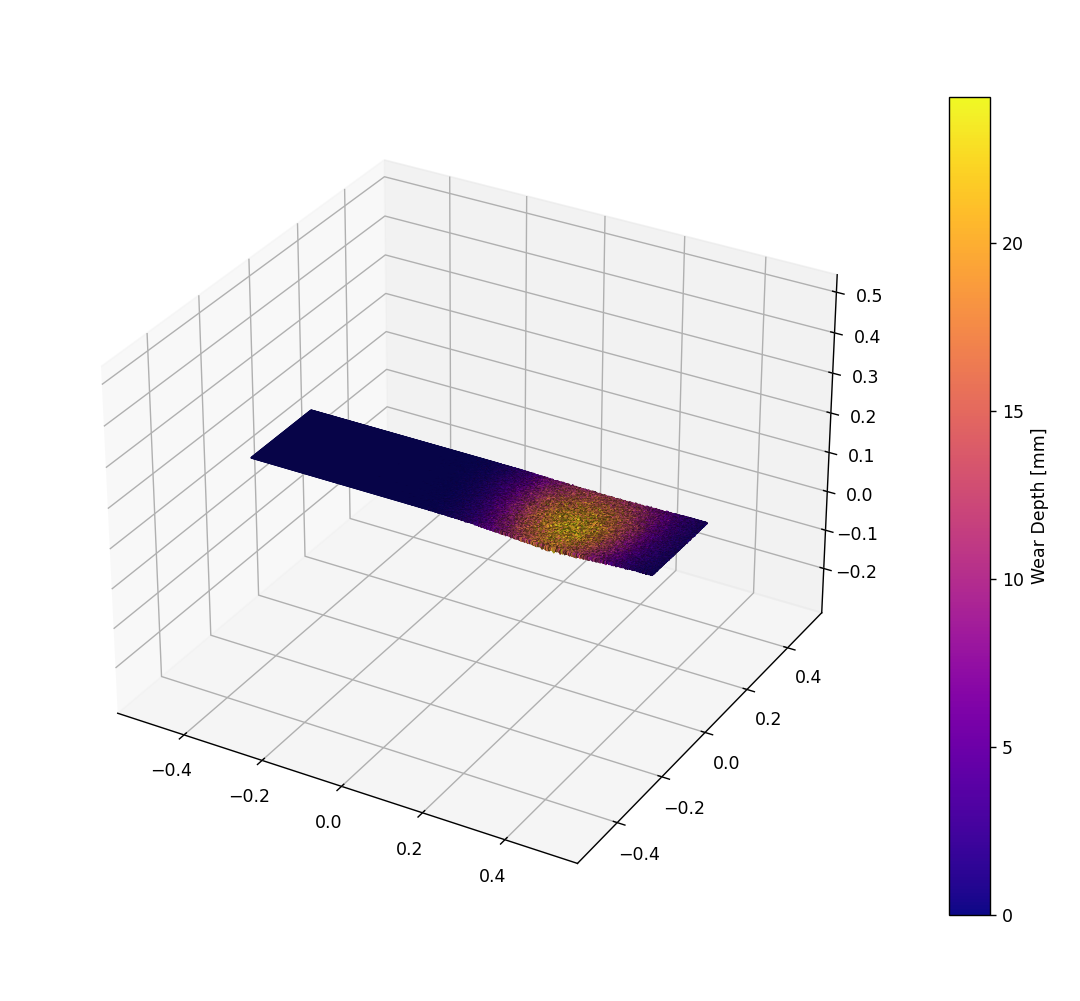
This year, we chose a problem focused on modeling wear on stairs, and using such wear patterns to
inform archaeologists to the age of the stairs, their usage patterns, and other quantities that
could be derived only from non-destructive measurements of the steps.
We chose to approach this by constructing an empirical distribution of footfalls on the stairs; from
this distribution (we used a Gaussian mixtured model), we backed out values such as the means and
covariances of the Gaussians which we then used to back out properties related to the age and usage
of the stairs.
We again won an Honorable Mention for our work.
Download our paper here, or view a repository with the paper and
code here!
Derivations and Applications of the Discrete, Fast, and Short-Time Fourier Transforms
My numerical analysis class included a final project that built on a topic we covered and presented
results we had not previously discussed.
I teamed up with two of my friends from the Engineering
Honors Program and we decided to study further the Fourier transform - an important tool in
signal processing, electronics, and many other fields.
As part of my work with the LAIR lab, I had been exposed to the
short-time Fourier transform, a tool used for generating spectrograms of time-varying signals; we
utilized this knowledge, as well as
Edward
Wawrzynek's experience working with frequency domain analysis, to explore the use cases of
the discrete, fast, and short-time Fourier transforms.
We used several real-life datasets in this study as well, studying both patterns in weather around
Boulder, Colorado and attempting to visualize some of the same EMIC waves I was studying in my
research!
Download our paper here, or check out our code
repository
here!
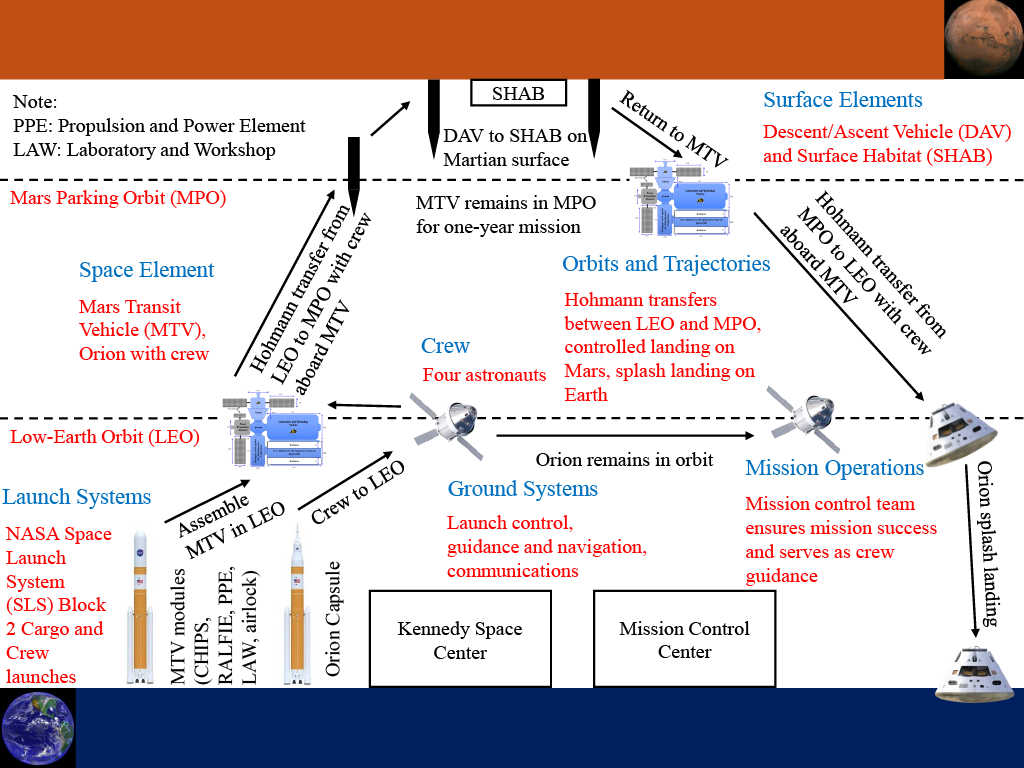
Design Proposal for Crewed Interplanetary Mission
As part of my Introduction to Human Spaceflight Class under former NASA astronaut Jim Voss, I wrote
a report detailing a living module and Environmental Control and Life Support Systems (ECLSS) for a
hypothetical crewed mission to Mars.
This report involved analyzing existing ECLSS technologies, deciding which were best fit for the
mission, conducting research on them, and explaining how they would be implemented in this mission.
Also included in the report is a concept of operations (CONOPS) and interior and exterior views of
the living module.
Download my paper here!

Applications of Covariance Matrices and Jacobians in Orbital Mechanics
My partner Audra Rissmeyer and I wrote this paper as our final
report for our applied matrix methods class.
The paper explored the concepts of observational covariance matrices, transformations between
celestial
coordinate systems, and transformations of covariance matrices (and why these transformations would
be done).
We used MATLAB functions provided by NASA CARA to run the transformations discussed in Alfano and
Vallado’s
Updated Analytical Partials for Covariance Transformations and Optimization and illustrated
covariance
through our own MATLAB visualizations. We also illustrated the difference between Cartesian and
equinoctial
covariance distributions and briefly explained the significance that these distributions have.
Download our paper here, or view a repository with
the paper and code here!
COMAP ICM 2023
As a member of a team of three, I participated in the Interdisciplinary
Contest in Modeling, a yearly competition in which thousands of teams around the world pick one
problem out of three (or a separate set of three for the closely-related Mathematical Contest in
Modeling), research the problem, develop a model to represent the situation at hand, and write a
paper with their results, all over the span of only 100 hours.
This year, my team tackled a problem regarding the United Nations' Sustainable Development Goals
(SDGs) and how to best prioritize them to create the most beneficial change over the next decade.
The paper won an Honorable Mention, meaning it was in the top 30% of papers submitted for that
particular problem; we also presented this paper at the
2023 SIAM Front Range Student Conference, and it
was accepted into the
2024 issue of the University of Colorado Honors
Journal.
Download our paper here, or view a repository with the paper and
code here!







